CONVECCION FORZADA EN TUBERIAS Y OBJETOS SUMERGIDOS.

Por Sanchez Molina Diego

Convección Forzada en tuberías y objetos sumergidos.

Si en vez de partir de un fluido estacionario que se agita por el mero efecto de las diferencias de temperatura, forzamos el movimiento relativo con otros medios, tenemos lo que se conoce como convección forzada. Si la velocidad relativa de partida es lo bastante grande, la que sería provocada por los cambios de temperatura se hace irrelevante. La «constante» de convección del modelo del enfriamiento de Newton se hace muy insensible a la temperatura. Además de esto, como la velocidad relativa puede ser muy grande, la eficacia de la convección forzada puede ser mucho mayor que la de la convección natural. Esto es algo que se tiene en cuenta, por ejemplo, al diseñar sistemas de refrigeración para dispositivos electrónicos: cuando la refrigeración es por convección natural —refrigeración pasiva—, la superficie necesaria para disipar el calor puede ser muchísimo mayor que la necesaria con un sistema de refrigeración por convección forzada.

La refrigeración por convección forzada puede funcionar cuando la convección natural ni siquiera es una opción, bien por cuestiones geométricas (quizá sería necesario un disipador enorme), bien por cuestiones físicas (como sucede en las cargas de pago de la Estación Espacial Internacional, donde la convección natural no es una opción por el entorno de microgravedad).

La convección forzada es un mecanismo de transferencia de calor entre una superficie y un fluido con movimiento que fluye alrededor de la misma, el cual es forzado a circular a través de esta por algún equipo donde se hace variar la presión del fluido de trabajo. La convección forzada se obliga al fluido a fluir mediante medios externos, como un ventilador o una bomba.

Transmisión de calor en un tubo circular.

Consideraciones referentes a las correlaciones.

Definición de h. (h₁, h_a y h_ln )

Existen varias maneras de definir el coeficiente de h de transferencia de calor.

• A partir de las diferencias de temperatura inicial
• A partir de la medida aritmética de las diferencias de temperatura en dos regiones diferentes del tubo
• A partir de la media logarítmica de las diferencias de temperatura en dos regiones diferentes del tubo.

Si las condiciones del fluido varían mucho, entonces se define una h_loc

Números adimensionales.

•       El Nu se construye con base en h por lo tanto también hay Nu₁, Nu_b, Nu_ln…

•       Tener cuidado con las escalas seleccionadas, por ejemplo: D, R_h , a (Volumen/área en lecho fluidizado), u otra para el Re.

•       Tener cuidado con los subíndices, por ejemplo f (temperatura de película)

T_f = (T₀ + T_∞)/2

Cilindro sumergido (Convección forzada).

El procedimiento para calcular la cantidad de calor transferida es:

•       Calcular el Reynolds, según los datos del problema.

•       Ir a la gráfica y leer el valor de J_H

•       Con el resto de los datos del problema calcular h.

Diámetro hidráulico (Tubos no circulares)

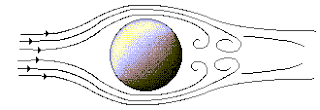Flujo sobre cilindros y esferas

·       Movimiento complicado de analizar analíticamente.

·       Se estudian experimentalmente o numéricamente.

Nussel promedio para el cilindro

De manera genérica:

Esfera sumergida: Convección forzada

Lecho fluidizado

●      Para el lecho fluidizado ( y otros problemas) se utilizan para h valores locales definidos en una sección transversal. 

●      En ese caso por ejemplo el Re puede definirse como     Re=G₀ /aµ_f ψ Con G₀ la velocidad másica y ψ un parámetro empírico que depende de la forma de las partículas del lecho.

Donde:

EJERCICIOS DEL TEMA:

https://paper.dropbox.com/doc/Practica-Semana-10.-Transferencia-de-calor-por-conveccion-forzada-en-tubos-y-alrededor-de-objetos-sumergidos.-PSQjoxuVJROROxCOe5ihU

CONVECCIÓN FORZADA ALREDEDOR DE PLACAS.

https://www.dropbox.com/s/im2ag8yeim5gcpt/Pr%C3%A1ctica_Semana_9_%20Introducci%C3%B3n%20a%20la%20Convecci%C3%B3n.pdf?dl=0

ESTADO ESTACIONARIO CON GRADIENTES (COORDENADAS CILINDRICAS)

ESTADO ESTACIONARIO CON GRADIENTES (COORDENADAS CILINDRICAS)

Elaborado por: Sara Flores Casarrubias

• La ecuación de difusión describe la conducción de calor en estado no estacionario, cuando no hay fuentes de generación de calor.

Donde α, la difusividad térmica, es el cociente k/ρCp

• Diferentes formas de escribir el Laplaciano según sus coordenadas:

Métodos para trabajar las soluciones:

• Analítico 
• Gráfico
• Excel
• Simuladores en Mathematica

Solución de la placa de espesor 2H

Cilindro Conductor. Separación de Variables:

 Ecuación de Bessel:

• Tiene una singularidad en el origen.
• Existe una infinidad de soluciones “etiquetadas” con un subíndice γ

Solución con la siguiente gráfica:

Relación condiciones de Frontera/Soluciones:

Las funciones de Bessel J (βmr ) son como las funciones de Fourier (Sen λn t y Cos λn t) que permiten escribir una función solución de una ecuación diferencial en derivadas parciales con condiciones a la frontera, como suma de ellas.

Las funciones de Bessel aparecen en problemas de simetría cilíndrica.

• Ejemplos a la solución de los diferentes métodos:

Gráfico

Excel

https://www.dropbox.com/s/v4ngegmigtlushg/Pr%C3%A1ctica%207.%20Transferencia%20de%20calor%20en%20r%C3%A9gimen%20no%20estacionario_cil%C3%ADndricas%2C%20EQUIPO%20AA.pdf?dl=0

TRANSFERENCIA DE CALOR EN ESTADO NO ESTACIONARIO

NO ESTACIONARIO

Elaborado por: Sara Flores Casarrubias

• Hasta esta parte del curso, los perfiles de temperatura que hemos visto no varían con el tiempo
• Eso se consigue gracias a que continuamente se proporciona energía al sistema (calefactor, por ejemplo) para compensar la pérdida.
• Lo “natural” sería que los perfiles cambiaran con el tiempo.

• ·         Tratamientos Térmicos

Son ciclos controlados de calentamiento y enfriamiento para provocar cambios en la microestructura.

Todas las reacciones de transformación de los aceros durante el enfriamiento desde la temperatura de austenización son exotérmicas

Eso resulta en el efecto conocido como recalescencia, que es el cambio de pendiente que se aprecia en la curva de enfriamiento

•  Difusión:

•  Número de Biot:

> 0.1 no se sostiene aproximidad

< 0.1 se sostiene aprox

• Velocidad de enfriamiento:

·       

•          Conductividad finita (Existencia de gradientes):

Donde α, la difusividad térmica, es el cociente 

k/ρC_p

 •      Para aplicarla a la solución de un caso particular es necesario fijar la:

        Geometría (Rectangular,  cilíndrica, 1D, 2D…)

Las condiciones iniciales y de frontera que lo describen.  

•          Solución analítica:

https://www.dropbox.com/s/ugofj8gis53hmvn/Pr%C3%A1ctica%206.%20Transferencia%20de%20calor%20en%20r%C3%A9gimen%20no%20estacionario%20%28Autoguardado%29.docx?dl=0

  

FUENTES INTERNAS

FUENTES INTERNAS

Elaborado por : Sara Flores Casarrubias

Balances sin Fuentes de Calor:

Velocidad de la entrada de energía calorífica – velocidad de salida de la energía   calorífica  = 0

Balances con Fuentes de Calor:

Velocidad de la entrada de energía calorífica – velocidad de salida de la energía   calorífica + Velocidad de producción de la energía calorífica  = 0

Efecto Joule

Se =  Velocidad de generación de energía por unidad de volumen

·         Calculo de Se:

• ·         Energía generada que con la diferencia de potencial y a la resistividad.

Ley de Fourier

      Ambas ecuaciones son parabólicas, sin embargo en la de la parte superior se toma en cuenta la diferencia de temperaturas, mientras que la de la parte inferior, nuestro  objetivo puede llegar a ser la obtención de la temperatura máxima. 

·         Ecuación para el incremento medio de la temperatura:

  Ley de Wiedemann- Franz:

      K/Ke = LT

    Donde: 

    L= Constante de Lorenz, con valor de 2.44x10^-8 W W K^-2

    T= Temperatura absoluta

     Relación de cocientes de conductividad: K/Ke

·         Ecuación para calcular el flujo de calor en la superficie:

·                    ·      Relación de q ´ con la intensidad:

Viscosidad

     Es la multiplicación de la viscosidad de los aceites, por la diferencia de las velocidades al cuadrado, un ejemplo claro se obseva que es la velocidad en z pero con dirección en el eje de las x.

Reacción química

   

   En donde se observa que  tanto Sc1 como T¯0, son constantes empíricas, las cuales les puedes dar cualquier valor al primer termino de la ecuación, y otro valor diferente a la temperatura.

   

    Se puede observar en el perfil de ecuaciones que es la suma de los exponenciales, esta función depende del material y de su geometría.

Reacción nuclear

    Se genera calor tanto en R_F, como en R_c donde

F= Material Fusionable

C= Material Encapsulable

b= velocidad con la que crecerá la parábola

IMPORTANTE:  Rc > R<sub>F


https://paper.dropbox.com/doc/Practica-4.-Generacion-interna-8cA9qEFUT2h18tSfpCxgu</sub>

PAREDES COMPUESTAS

PAREDES COMPUESTAS

Hecho por Rodríguez Jiménez Brenda Daniela

Donde el flujo de calor esta descrito desde T1 hasta T4 pasando por distintos espesores de materiales distintos,  donde la caída de temperatura al paso de cada uno de ellos esta descrito por el perfil de temperaturas (línea purpura).

Donde el flujo de calor esta descrito desde T1 hasta T4 pasando por distintos espesores de materiales distintos,  donde la caída de temperatura al paso de cada uno de ellos esta descrito por el perfil de temperaturas (línea purpura)

  

La ecuación que describe la  trasferencia de calor por ese perfil de temperaturas está referida a la ley de Fourier.

Generando un balance de energía para un sistema estacionario sin acumulación se tiene que la cantidad de energía trasferida por una unidad de área para un volumen de control (Flux) de entrada es igual al Flux de salida.

De esta manera tenemos que la trasferencia de calor para un sistema de paredes planas compuestas donde existen trasferencias de energía convectivas con un medio y conductivas por el espesor de las paredes esta descrita por la siguiente ecuación.

En donde las Ta y Tb refieren a las temperaturas del medio en el los extremos “fríos” y “calientes”, los términos dependientes de h refieren a las pérdidas de calor por convección y los dependientes de K refieren a la trasferencias de calor por conducción a través de la oposición de los diferentes materiales; todas estos términos igualados al flux total de calor del extremo “frío” al extremo “caliente”.

Si no se tienen perdidas de calor por convección entonces la ecuación queda en términos solo de la resistencia de los materiales al trasporte de calor, es decir, K y los términos convectivos, en función de h, son igual a cero, teniendo: 

CONDUCCIÓN DE CALOR POR PAREDES COMPUESTAS PARA UN CILINDRO. 

De la misma forma, la transferencia de calor para un cilindro esta descrita por las mismas ecuaciones, solo que este caso se debe considerar un área variable para cada punto desde el centro del cilindro hacia la superficie.

 Por lo cual se tiene que la transferencia de calor ahora está referida en función de un radio r variable en cada punto del cilindro, por lo cual la caída de calor por cada capa del cilindro es de forma exponencial, teniendo:

Para donde se asocia un valor de K especifico de cada material, el que, al tener un espesor definido también presenta una caída de energía logarítmica en función de la posición del radio de referencia hasta un punto r2. 

Para definir el perfil de temperatura para este caso (cuadro verde).

La convección en las fronteras.

De esta manera la ecuación de continuidad que describe la trasferencia de calor para un cilindro de radio R con paredes compuestas y perdidas de energía es la anterior. 

https://paper.dropbox.com/doc/Practica-3.-Paredes-compuestas-67s3JiXixnVZk1dkkDJhF